Содержание
I.Введение
II.Основная часть
2.1.Основные понятия теории уравнений и неравенств
2.2.Методы решения уравнений и неравенств
2.3.Нестандартные методы решения алгебраических уравнений и неравенств
2.4.Нейросеть- как инновация в решении уравнений и неравенств по математике
2.5.Опрос школьников на предмет проблем в решении уравнений и неравенств
2.6.Разработка тренажера «Нестандартные методы решения уравнений и неравенств»
2.7.Нейросеть «01Математика»-как наиболее удобный формат для обучения
2.8.Апробация продукта
III. Заключение
IV.Список литературы
Доклад
Уважаемые члены комиссии! Вашему вниманию предлагается исследовательская работа на тему: «Нестандартные методы решения уравнений и неравенств»( слайд 1)
Содержание
Структурно исследовательская работа состоит из введения, основной части, заключения, списка использованных источников (слайд 2)
I.Введение(слайд 3)
Актуальность исследования. На ЕГЭ очень важно правильно распределять и экономить время, поэтому для успешной сдачи экзамена требуются новые методы решения, обеспечивающие наиболее быстрое выполнение заданий. На занятиях математики в школе учащиеся сталкиваются с такой проблемой – способы решения данных заданий, изучаемые в школе, зачастую занимают много времени, что говорит о нехватке знаний о наиболее оптимальных способах решения уравнений и неравенств.
Объектом исследования являются школьники 9-11 классов.
Предмет исследования: стандартные и нестандартные методы решения уравнений и неравенств.
Гипотеза: благодаря новым методам решения уравнений и неравенств, появится возможность сократить количество шагов решения в алгоритме и снизить вероятность допущения ошибки.
Исходя из этого, была поставлена цель исследования: изучить новые методы решения уравнений и неравенств.
Для достижения указанной цели, необходимо решить следующие задачи:
1)Изучить теоретические аспекты стандартных и нестандартных методов решения уравнений и неравенств.
2)Провести опрос школьников на предмет изучения методов решений уравнений и неравенств.
3)Разработать тренажер для наилучшего обучения решения уравнений и неравенств в математике, в том числе и при подготовке к ЕГЭ.
4) Опробировать тренажер и провести опрос школьников об эффективности продукта.
Методами исследования являются: анализ, обобщение, синтез, классификация, систематизация, сравнение.
Практическая значимость: продукт проекта может быть использован учениками при подготовке к ЕГЭ.
Социальная значимость: проект может помочь ученикам 9-11 классов при подготовке к экзамену.II.Основная часть
2.1.Основные понятия теории уравнений и неравенств
(слайд 4)Рассмотрим основные понятия теории уравнений и неравенств.
Уравнение – равенство, содержащее в себе переменную, значение которой требуется найти.
Корень (решение) уравнения – это значение переменной, при котором уравнение обращается в верное числовое равенство.
Решить уравнение – найти его корни или доказать, что корней нет.
Неравенство – два числа или математических выражения, соединенных одним из знаков: <, >, ?, ?.
Основные свойства уравнений:
-Любой член уравнения можно перенести из одной части в другую, изменив его знак на противоположный.
-Обе части уравнения можно умножить или разделить на одно и то же число, не равное нулю.
Решение неравенства – то значение неизвестного, при котором это неравенство обращается в верное числовое неравенство.
Решить неравенство – найти все его решения или установить, что их нет.[9]2.2.Методы решения уравнений и неравенств(слайд 5)
Теперь, после перечисления основных понятий, следует вспомнить известные из школьной программы способы решения уравнений и неравенств.
Метод разложения на множители.
Для разложения на множители используют формулы сокращённого умножения (ФСУ), вынесение общего множителя за скобку, способ группировки, деление многочлена на многочлен.
Суть данного метода в том, чтобы путем равносильных преобразований представить левую часть исходного уравнения, содержащую неизвестную величину в какой-либо степени, в виде произведения двух выражений, содержащих неизвестную величину в меньшей степени. При этом справа от знака равенства должен оказаться ноль.
Метод замены переменной.
Цель данного метода в том, чтобы удачным образом заменить сложное выражение, содержащее неизвестную величину, новой переменной, в результате чего уравнение принимает более простой вид. Далее полученное уравнение решается относительно новой переменной, после чего происходит возврат к исходной переменной.
Метод решения уравнений с помощью теоремы Виета.
Не ко всем квадратным уравнениям имеет смысл использовать эту теорему. Применять теорему Виета имеет смысл только к приведённым квадратным уравнениям.
Приведенное квадратное уравнение – это уравнение, в котором старший коэффициент «a = 1». В общем виде приведенное квадратное уравнение выглядит следующим образом: х2 + px + q = 0. разница с обычным общим видом квадратного уравнения ax2 + bx + c = 0 в том, что в приведённом уравнении x2 + px + q = 0 коэффициент а = 1.
Теорема Виета для приведённых квадратных уравнений «x2 + px + q = 0» гласит что справедливо следующее:
x1 + x2 = ?p, x1 • x2 = q, где x1 и x2 — корни этого уравнения.[7]2.3.Нестандартные методы решения алгебраических уравнений и неравенств (слайд 6)
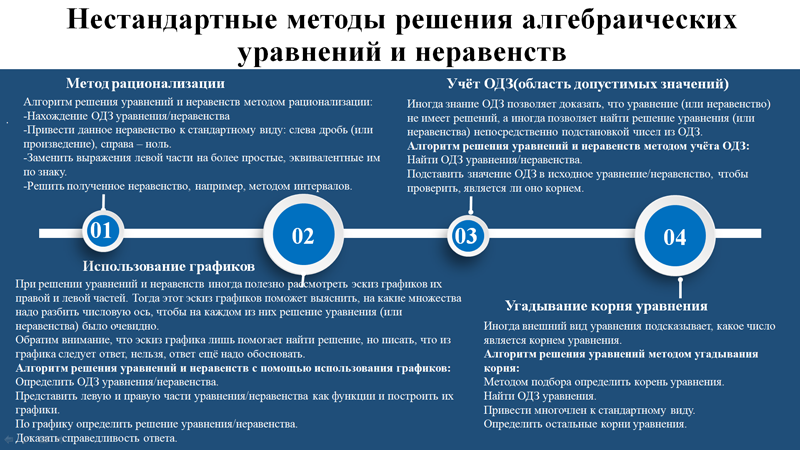
1)Метод рационализации.
Алгоритм решения уравнений и неравенств методом рационализации:
-Нахождение ОДЗ уравнения/неравенства
-Привести данное неравенство к стандартному виду: слева дробь (или произведение), справа – ноль.
-Заменить выражения левой части на более простые, эквивалентные им по знаку.
-Решить полученное неравенство, например, методом интервалов.
2)Учёт ОДЗ(область допустимых значений).
Иногда знание ОДЗ позволяет доказать, что уравнение (или неравенство) не имеет решений, а иногда позволяет найти решение уравнения (или неравенства) непосредственно подстановкой чисел из ОДЗ.
Алгоритм решения уравнений и неравенств методом учёта ОДЗ:
-Найти ОДЗ уравнения/неравенства.
-Подставить значение ОДЗ в исходное уравнение/неравенство, чтобы проверить, является ли оно корнем.
3)Использование графиков.
При решении уравнений и неравенств иногда полезно рассмотреть эскиз графиков их правой и левой частей. Тогда этот эскиз графиков поможет выяснить, на какие множества надо разбить числовую ось, чтобы на каждом из них решение уравнения (или неравенства) было очевидно.
Обратим внимание, что эскиз графика лишь помогает найти решение, но писать, что из графика следует ответ, нельзя, ответ ещё надо обосновать.
Алгоритм решения уравнений и неравенств с помощью использования графиков:
-Определить ОДЗ уравнения/неравенства.
-Представить левую и правую части уравнения/неравенства как функции и построить их графики.
-По графику определить решение уравнения/неравенства.
-Доказать справедливость ответа.
4)Угадывание корня уравнения.
Иногда внешний вид уравнения подсказывает, какое число является корнем уравнения.
Алгоритм решения уравнений методом угадывания корня:
-Методом подбора определить корень уравнения.
-Найти ОДЗ уравнения.
-Привести многочлен к стандартному виду.
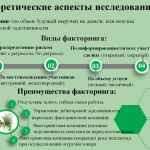
-Определить остальные корни уравнения.[1]2.4.Нейросеть- как инновация в решении уравнений и неравенств по математике (слайд 7)
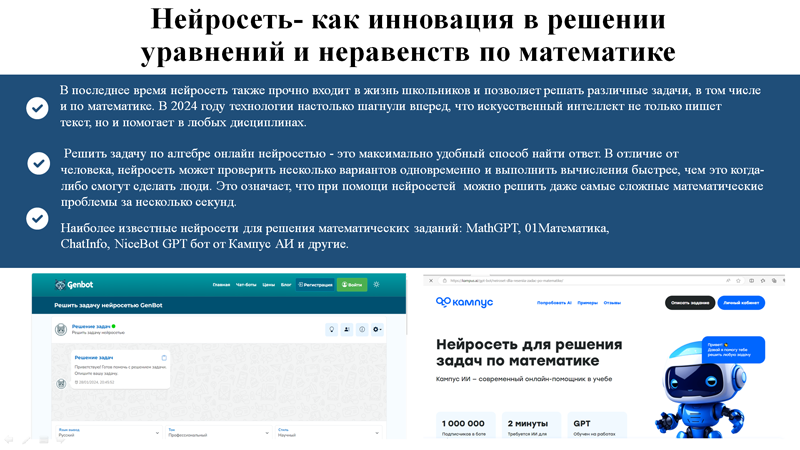
В последнее время нейросеть также прочно входит в жизнь школьников и позволяет решать различные задачи, в том числе и по математике. В 2024 году технологии настолько шагнули вперед, что искусственный интеллект не только пишет текст, но и помогает в любых дисциплинах.
Решить задачу по алгебре онлайн нейросетью – это максимально удобный способ найти ответ. В отличие от человека, нейросеть может проверить несколько вариантов одновременно и выполнить вычисления быстрее, чем это когда-либо смогут сделать люди. Это означает, что при помощи нейросетей можно решить даже самые сложные математические проблемы за несколько секунд.
Наиболее известные нейросети для решения математических заданий: MathGPT, 01Математика, ChatInfo, NiceBot GPT бот от Кампус АИ и другие.[8] [6][4]2.5.Опрос школьников на предмет проблем в решении уравнений и неравенств(слайд 8)
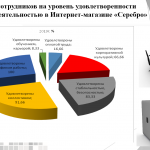
Для определения потребности школьников по совершенствованию методов решения уравнений и неравенств был проведен опрос среди школьников 9-11 классов. Всего было опрошено 28 человек. Опрос показал, что у 69,23% возникают трудности с решением уравнений и неравенств.
Также было выявлено, что самые распространенные проблемы при решении уравнений и неравенств среди учеников – проблема с выбором рационального решения и неочевидное решение. Более того, в результат опроса показал, что ни один школьник не использует нейросеть для обучения и решения уравнений и неравенств и только 1 человек применяет различные обучающие интернет-ресурсы для решения математических уравнений и неравенств.
Результатами опроса подтвердился также выбор формата продукта. 85,71% опрошенных отметили, что им было бы удобно практиковаться в предложенной теме в формате онлайн- тренажера, что в итоге и было выбрано продуктом проекта.2.6.Разработка тренажера «Нестандартные методы решения уравнений и неравенств» (слайд 9)
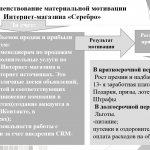
Для наилучшего восприятия информации и повышения обучаемости школьников был создан информационный продукт, который объединяет теорию и тренажёры (упражнения) в одну презентацию.
Презентация. Основная задача презентации заключается в наглядном представлении алгоритмов решения уравнений/неравенств, примеров решения, а также в размещении ссылок на онлайн-тренажёры для каждого метода.
Тренажёр. Для каждого метода решения уравнений/неравенств имеются несколько онлайн тренажёров (упражнений): на проработку алгоритма, проработку ключевых формул и на тренировку самого решения.[5]
Нейросети.Также рекомендуется применение нейросетей, которые позволяют обучать школьников и подготавливаться к ЕГЭ по математике. Такой нейросетью является «01Математика».[10]2.7.Нейросеть «01Математика»-как наиболее удобный формат для обучения (слайд 10)
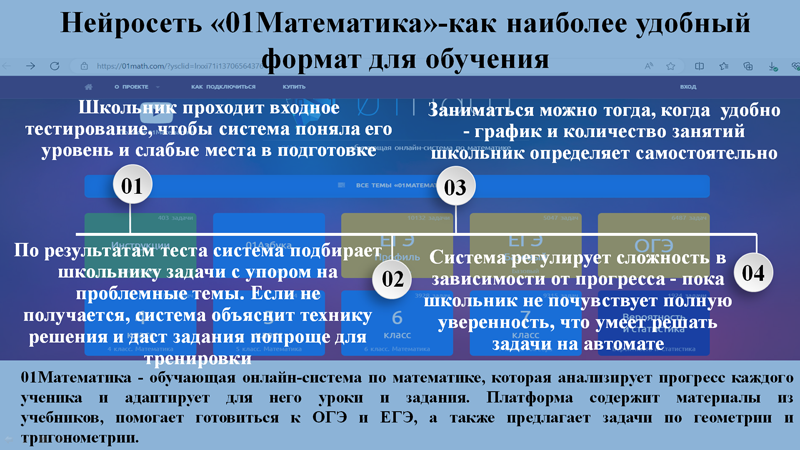
01Математика – обучающая онлайн-система по математике, которая анализирует прогресс каждого ученика и адаптирует для него уроки и задания. Платформа содержит материалы из учебников, помогает готовиться к ОГЭ и ЕГЭ, а также предлагает задачи по геометрии и тригонометрии.
В нейросети «01Математика» происходит все следующим образом:
1)Школьник проходит входное тестирование, чтобы система поняла его уровень и слабые места в подготовке;
2)По результатам теста система подбирает задачи с упором на проблемные темы. Если не получается, система объяснит технику решения и даст задания попроще для тренировки;
3)Заниматься можно тогда, когда удобно – график и количество занятий школьник определяет самостоятельно.
4)Система регулирует сложность в зависимости от прогресса – пока школьник не почувствует полную уверенность, что умеет решать задачи на автомате.[10]2.8.Апробация продукта(слайд 11)
После создания продукта была проведена его апробация среди учеников 9-11-х классов, которая позволила провести оценку тренажёра относительно поставленных ранее критериев и ввести коррективы для его лучшей работы.
После представления тренажера были предоставлены следующие результаты опроса: все школьники считают, что данный продукт соответствует заявленной теме, все информация, которая представлена в презентации тренажере понятна, данный тренажер является эффективным для всех опрошенных школьников.III. Заключение (слайд 12)
В данной работе были исследованы некоторые нестандартные методы решения уравнений и неравенств. Представленный опрос школьников 9-11 классов показал, что многие испытывают трудности при решении уравнений и неравенств, практически никто не применяет нейросети и интернет-ресурсы для подготовки к экзаменам и решению математических уравнений и неравенств. Большинство опрошенных считают, что тренажер-презентация был бы полезен для решения проблемы с уравнениями и неравенствами. В ходе проекта был создан тренажер, который представляет собой объединение теории и практики в одну презентацию. В презентации представлены алгоритмы решения уравнений/неравенств, примеров решения, а также размещены ссылки на онлайн-тренажёры для различных методов. Кроме этого, в данном продукте делается акцент на применение нейросети –«01Математика» —которая анализирует прогресс каждого ученика и адаптирует для него уроки и задания. Платформа помогает готовиться к ОГЭ и ЕГЭ, а также предлагает задачи по геометрии и тригонометрии.
Подводя итог данной теме, стоит отметить, что использование нестандартных методов решения уравнений и неравенств, к сожалению, отодвигается на второй план, несмотря на то, что данные способы являются наиболее эффективными в решении. Именно поэтому необходимо изучать данные методы, ведь они в действительности являются незаменимыми при решении уравнений и неравенств.IV.Список литературы(слайд 13)
1.Олехник С.Н., Потапов М.К., Пасиченко П.И. Уравнения и неравенства. Нестандартные методы решения: справочник. 1997. – 219 с.
2.Решить задачу нейросетью[Электронная версия][Ресурс: https://chatinfo.ru/reshit-zadachu-online?ysclid=lrxqdlp6i7389789043]
3.Решить задачу онлайн нейросетью | NiceBot[Электронная версия][Ресурс: https://nicebot.ru/reshit-zadachu-neirosetiy?ysclid=lrxqrk6nq0198848471]
4.Решить задачу онлайн [нейросеть] | ChatInfo[Электронная версия][Ресурс:https://chatinfo.ru/reshit-zadachu-online?ysclid=lrxqdlp6i7389789043]
5.Ссылки на ресурсы для дистанционного обучения по математике в 10-11 классах[Электронная версия][Ресурс: https://anna-kobets.ru/index.php/metodicheskie-materialy/245-ssylki-na-resursy-dlya-distantsionnogo-obucheniya-po-matematike-v-10-11-klassakh?ysclid=lrxnci2b84129205908]
6.Искусственный интеллект в образовании: перспективы и примеры использования [Электронная версия][Ресурс: https://media.foxford.ru/articles/neyroseti-v-obrazovanii?ysclid=lrxwzbtq5e66662795]
7.Колягин Ю. М., Ткачева М. В., Федорова Н. Е., Шабунин М. И. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс: базовый и углубленный уровни. 7-е изд. М.: Просвещение, 2019. – 384 с.
8.Нейросеть для решения задач по математике онлайн – GPT бот от Кампус АИ [Электронная версия][Ресурс:
https://kampus.ai/gpt-bot/neiroset-dlia-reseniia-zadac-po-matematike/]
9. Основные понятия теории уравнений и неравенств. [Электронная версия][Ресурс: https://multiurok.ru/files/1-osnovnyie-poniatiia-tieorii-uravnienii-i-nieravi.html?ysclid=ls25b56gwp772733918];
10.01Математика – обучающая онлайн-система по математике [Электронная версия][Ресурс: https://01math.com/?ysclid=ls255nexj2186424592].Спасибо за внимание! (слайд 14)
Титульный слайд (слайд 15)